机器学习 - 概率无向图模型

概率无向图模型，aka Markov 随机场（Markov Random Field）

无向图的因子分解#

有向图中我们分析了独立性，无向图这里也需要。有三种等价表示

• 局部 Markov 性：若某个顶点的所有邻居都已知（也即被观测），那么它与其他顶点条件独立
• 成对 Markov 性：若两个顶点之间没有直接相连，那么当其他所有顶点都已知时，这两个顶点条件独立
• 全局 Markov 性：若两个点集之间的通路都必须经过某个第三点集，那么当第三点集已知时，这两个点集之间条件独立

如果两个顶点被观测顶点分割的情况下条件独立，则这个无向图就称为 Markov 随机场

分析概率无向图时同样要做因子分解，但“无向”写不出有向图那样的依赖关系，因此需要使用最大团来做因子分解。备忘：团 (clique) 又称完全子图，即其中的任意两个顶点都有边连接。“最大团”即包含顶点数最多的团。

势函数#

这个分布也叫做 Gibbs 分布。

特别地，如果定义势函数 $\varphi_C(X_C)=\exp(-E_C(X_C))$，则称为 Boltzmann 分布，其中 $E$ 表示能量。

势函数求 Gibbs 分布例题#

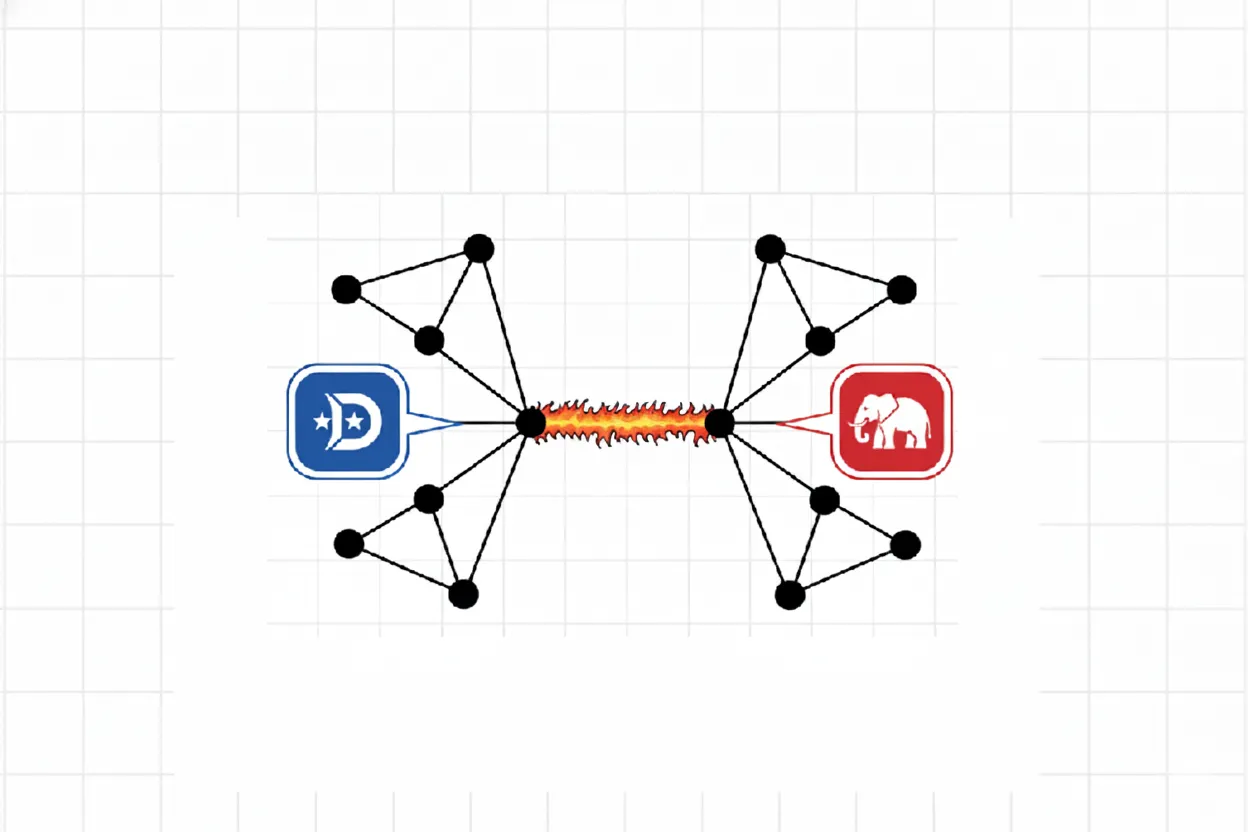
例题。总统大选中，共有懂王、拜登两位候选人。有 ABCD 四个人，他们四个人的关系网如下，连线表示两个人的投票倾向之间存在相互影响：

图中总共有四个团：AB、BC、CD、DA，都含有两个顶点，因此都是最大团。在这四个最大团上，定义相互影响的势函数为：

其中，事件“A 投懂王”为 $A=a^0$，“A 投拜登”为 $A=a^1$，其他类推。

势函数表反映了两人之间具体的影响关系。例如可以看出，BC、DA 很可能投同一个人，而 CD 很可能投不同的人。

于是 Gibbs 分布可以由下表计算得到。Gibbs 分布即归一化的势函数积，归一化系数就是中间那一列全部加起来

这就求出了联合分布。

从联合分布中可以得出边缘分布。例如我们求 AB 的边缘分布：

可以看出，全局联系改变了 AB 之间单独的关系。细究起来，这种变化主要来源于 CD 之间的强烈不一致性。

---

下面讲 3 个常用的概率无向图模型

logistic 回归模型#

说是回归，但其实是基于回归的分类模型。本章我们先用一般流程在二分类上做说明，再阐述多分类问题，以及它与概率无向图的关系

二分类与sigmoid#

基本推导#

传统的线性回归做分类，就是把正类样本设标签 $y=1$，负类样本设标签 $y=0$，然后得出线性拟合函数 $z=w^\mathrm{T}x$（偏置项通过 $b=[{w^{(0)}}]^\mathrm{T}x^{(0)}$ 塞进 $w^\mathrm{T}x$ 中）；对于测试样本，若拟合值大于某个值（比如 0.5），就分为正类，否则分为负类，这样就分出来了。这本质上是一个分段判别函数：

$$y=\begin{cases} 1,&z>0.5\\ 0,&z\leq 0.5 \end{cases}$$

它不连续，不可导。而 logistic 回归做分类，就是在传统的线性回归当中，加入了一个性质足够好判别函数。sigmoid 函数（aka logistic 函数）就是一个不错的选择：

$$y=\sigma(z)=\dfrac{1}{1+\mathrm{e}^{-z}}$$

它单增、任意阶可导，关于点 $(0,\ 0.5)$ 对称；另外，sigmoid 相当于一个 $\mathbb{R}\to [0,1]$ 的映射，或者说把实数轴映射成概率。于是 sigmoid 的结果便可以解释为：回归出来的数越大，分类为正类的概率就越大。

将样本 $x_{i}$ 分类为正类的概率记为 $p_i$，即

$$p_i=\sigma(w^\mathrm{T}x_i)=\dfrac{1}{1+\exp(-w^\mathrm{T}x_i)}$$

于是该样本分类正确的概率即为 $p_i^{y_i}(1-p_i)^{1-y_i}$；若进一步假设分类结果只与特征有关，那么全部分类正确的概率即为 $\prod_i p_i^{y_i}(1-p_i)^{1-y_i}$

于是我们的目标就是最大化对数似然函数：

$$\begin{aligned} L(w)&=\log\left[\prod\limits_i p_i^{y_i}(1-p_i)^{1-y_i}\right]\\ &=\sum\limits_i\big(y_i\log p_i+(1-y_i)\log(1-p_i)\big)\\ &=\sum\limits_i\big(y_i\log \dfrac{p_i}{1-p_i}+\log(1-p_i)\big)\\ \end{aligned}$$

这样变形的目的，是为了凑出对数几率函数 $\mathrm{logit}(p)=\log \dfrac{p}{1-p}$，因为它是 sigmoid 的反函数，而这里 $p=\sigma(w^\mathrm{T}x)$，故 $\log \dfrac{p}{1-p}$ 就等于 $w^\mathrm{T}x$（因此 logistic 回归也称为对数几率回归）。于是代入后继续化简得

$$\begin{aligned} L(w)&=\sum\limits_i\left[y_i(w^\mathrm{T}x_i)+\log\dfrac{\exp(-w^\mathrm{T}x_i)}{1+\exp(-w^\mathrm{T}x_i)}\right]\\ &=\sum\limits_i\big[w^\mathrm{T}x_iy_i-w^\mathrm{T}x_i-\log\big(1+\exp(-w^\mathrm{T}x_i)\big)\big]\\ \end{aligned}$$

梯度下降之即可。其中对 $w$ 的偏导可以进一步化简：

$$\begin{aligned} \dfrac{\partial L}{\partial w}&=\sum\limits_i\big[x_iy_i-x_i-\dfrac{-x_i\exp(-w^\mathrm{T}x_i)}{1+\exp(-w^\mathrm{T}x_i)}\big]\\ &=\sum\limits_ix_i\big[y_i-1+\dfrac{\exp(-w^\mathrm{T}x_i)}{1+\exp(-w^\mathrm{T}x_i)}\big]\\ &=\sum\limits_ix_i\big[y_i-\dfrac{1}{1+\exp(-w^\mathrm{T}x_i)}\big]\\ &=\sum\limits_ix_i\big[y_i-\sigma(w^\mathrm{T}x_i)\big]\\ \end{aligned}$$

把偏置项拆出来，即

$$\begin{aligned} \frac{\partial L}{\partial w} &= \sum_i x_i [y_i - \sigma(w^\mathrm{T}x_i + b)]\\ \frac{\partial L}{\partial b} &= \sum_i [y_i - \sigma(w^\mathrm{T}x_i + b)] \end{aligned}$$

至于最后如何判别，就是看分类为正类的概率是否比负类大，本质上还是和 0.5 比大小，但这种比大小可以从概率角度解释，和传统的回归分类还是有区别的；由 sigmoid 单调性，也可以等价为 $w^\mathrm{T}x$ 和 0 比大小。

交叉熵损失#

实践中采用 mini-batch 梯度下降，即在小批量样本上（而不是在整个训练集上）做梯度下降。为了防止样本量对 loss 的数值尺度的影响，需要把损失函数除以样本量，也即定义损失函数

$$J(w) = - \dfrac{1}{m} L(w) = -\dfrac 1m\sum\limits_{i=1}^m\bigg[y_i\log p_i+(1-y_i)\log(1-p_i)\bigg]$$

这称为交叉熵损失。其中 $y_i$ 是第 $i$ 个样本的真实标签，取值 0 或 1，$p_i$ 是模型预测该样本为正类的概率。

为什么跟“熵”有关系：从公式的形式来看，它是概率的负对数的平均值，这相当于求“在所有样本的真实标签都已知时，获得的信息量的期望”。这个信息量越小，说明“真实标签”这个信息越没用，也即表明模型预测的概率分布越准确，离真实标签的差异越小。

另外实践中，为了防止对 0 取对数，需要在 log 里面加上一个小正数 $\varepsilon$

多分类与 softmax#

多分类的思路和 logistic 是一样的，只不过它使用权重矩阵 $W=[w_i]$ 代替刚才的权重向量 $w$（同样的，偏置项 $b_k$ 塞进 $w_k$ 的第 0 项），得到“分为每个类的打分”：

$$z_k=w_k^\mathrm{T}x$$

然后再用 softmax 函数将 $\vec{z}$ 压成分类结果的概率分布向量 $\vec{p}$：

$$p_k = P(y=k|\vec{z}) = \text{softmax}_k(\vec{z}) = \dfrac{\exp(z_k)}{\sum_{j=1}^K\exp(z_j)}$$

对于多分类问题，loss 函数仍然是用“全部分类正确的概率”然后取对数平均（也即交叉熵）：

$$L(W) = -\dfrac{1}{m}\sum_{i=1}^my_{i}^\mathrm{T}\log p_{i}$$

其中第 $i$ 样本的真实标签 $y_i$ 是 onehot 编码，例如对于三分类问题，标签“1”、“2”、“3”分别表示为 $[1,0,0]^\mathrm{T}$、$[0,1,0]^\mathrm{T}$ 和 $[0,0,1]^\mathrm{T}$。

loss 梯度计算#

仍然需要使用梯度下降进行优化。回顾 logistic 回归中，求 loss 的梯度时是通过配凑 logit 来化简的。softmax 回归中也需要做类似的化简，以便于计算 loss 的梯度。

softmax 把向量映射成向量，相当于向量值函数，其关于自变量 $\vec z$ 的偏导应该是一个 Jacobi 矩阵。记 softmax 结果为 $\vec p$，也即

$$p_k(\vec{z}) = \dfrac{\exp(z_k)}{\sum_{k=1}^K\exp(z_k)}$$

于是在求“分为第 $k$ 类的概率”关于“第 $j$ 类的打分”$\dfrac{\partial p_k}{\partial z_j}$ 时，显然可以分类讨论：

1. 当 $j\neq k$ 时，自变量只在分母出现。求导时，分母平方；分子“上导下不导”中，上导为 0、“下导上不导”等于 $\exp(z_j)\exp(z_k)$，于是求导结果即为

$$\frac{\partial p_k}{\partial z_j}=\frac{-\exp(z_j)\exp(z_k)}{\big(\sum_{k=1}^K\exp(z_k)\big)^2}=-p_jp_k$$

2. 当 $j=k$ 时，“上导下不导”等于 $\exp(z_j)(\Sigma)$、“下导上不导”等于 $\exp^2(z_j)$，于是求导结果即为

$$\frac{\partial p_k}{\partial z_j}=\frac{\exp(z_j)(\Sigma)-\exp^2(z_j)}{(\Sigma)^2}=\frac{\exp(z_j)}{\Sigma}-\left(\frac{\exp(z_j)}{\Sigma}\right)^2=p_j-p_j^2=p_j(1-p_j)$$

---

有了这些之后就可以计算 loss 的梯度。为了表述清晰，我们先关注单个样本的 loss 关于打分的偏导，然后再推广到整个数据集在模型参数上的偏导。由于求导过程涉及对自变量向量的非线性运算，需要把第 $i$ 样本的 loss 中的向量点乘写开来：

$$L_i = -y_i^\mathrm{T} \log p_i = - \sum_{k=1}^K y_{ik} \log p_{ik}$$

其中 $y_{ik}$ 是第 $i$ 个样本的真实标签的第 $k$ 分量，$p_{ik}$ 是模型预测第 $i$ 个样本分为第 $k$ 类的概率。于是由链式法则，第 $i$ 样本的损失 $L_i$ 对第 $j$ 类的打分 $z_{ij}$ 的偏导为

$$\begin{aligned} \frac{\partial L_i}{\partial z_{ij}} &= \frac{\partial L_i}{\partial p_{ik}} \frac{\partial p_{ik}}{\partial z_{ij}}=-\sum_{k=1}^K \frac{y_{ik}}{p_{ik}} \frac{\partial p_{ik}}{\partial z_{ij}}\\ &= \underbrace{\left( -\frac{y_{ij}}{p_{ij}} \frac{\partial p_{ij}}{\partial z_{ij}} \right)}_{k=j} + \sum_{k \neq j} \underbrace{\left( -\frac{y_{ik}}{p_{ik}} \frac{\partial p_{ik}}{\partial z_{ij}} \right)}_{k \neq j} \\ &= \left( -\frac{y_{ij}}{p_{ij}} \right) \cdot \big( p_{ij}(1-p_{ij}) \big) + \sum_{k \neq j} \left( -\frac{y_{ik}}{p_{ik}} \right) \cdot (-p_{ij}p_{ik}) \\ &= -y_{ij}(1-p_{ij}) + \sum_{k \neq j} y_{ik}p_{ij} \\ &= -y_{ij} + y_{ij}p_{ij} + p_{ij}\sum_{k \neq j} y_{ik} \\ &= -y_{ij} + p_{ij} \sum_{k=1}^K y_{ik} \end{aligned}$$

而对于 onehot 编码向量 $y_i$ 而言，$\sum\limits_{k=1}^K y_{ik}\equiv1$，于是

$$\frac{\partial L_i}{\partial z_{ij}} = p_{ij} - y_{ij}$$

代入 $z_{ij}=w_{j}^\mathrm{T}x_i+b_j$ 得

$$\frac{\partial L_i}{\partial w_j} = \frac{\partial L_i}{\partial z_{ij}} \frac{\partial z_{ij}}{\partial w_j} = (p_{ij} - y_{ij}) x_i$$

最后只需要将所有样本的梯度进行平均，于是总 loss 对参数的梯度

$$\frac{\partial L}{\partial w_j} = \frac{1}{m} \sum_{i=1}^m (p_{ij} - y_{ij}) x_i$$

拆出偏置项的形式：

$$\begin{aligned} \frac{\partial L}{\partial w_j} &= \frac{1}{m} \sum_{i=1}^m (p_{ij} - y_{ij}) x_i\\ \frac{\partial L}{\partial b_j} &= \frac{1}{m} \sum_{i=1}^m (p_{ij} - y_{ij}) \end{aligned}$$

对比：logistic 回归中，采用交叉熵损失时的 loss 梯度 $\dfrac{\partial L}{\partial w}=\dfrac1m\displaystyle\sum\limits_ix_i\big[\sigma(w^\mathrm{T}x_i)-y_i\big]$，其中 $\sigma$ 那一项就是概率，因此在形式上是完全一样的

无向图模型视角#

现在我们回头用概率无向图模型的观点来审视 logistic 回归。事实上，logistic 回归可以被看作一个非常简单的 Markov 随机场。

考虑一个分类问题，我们有输入特征 $X=\{X_1, \dots, X_d\}$ 和输出类别 $Y$。构建一个无向图，其中 $Y$ 和所有的 $X_i$ 都相连，所有 $X_i$ 之间也相互连接。这个图本身就是一个巨大的团，也是该图的唯一最大团。于是分类问题即求条件概率 $P(Y=k\mid X=\vec x)$

根据 Hammersley-Clifford 定理，该图的联合概率分布可以表示为：

$$P(Y, X) = \frac{1}{Z}\varphi(Y, X)$$

于是条件概率

$$P(Y\mid X) = \frac{P(Y, X)}{P( X)} = \frac{P(Y, X)}{\sum_{Y'}P(Y', X)} = \frac{\frac{1}{Z}\varphi(Y, X)}{\sum_{Y'}\frac{1}{Z}\varphi(Y', X)} = \frac{\varphi(Y, X)}{\sum_{Y'}\varphi(Y', X)}$$

如果定义势函数

$$\varphi(Y, X) = \exp\left( \sum_{k=1}^K \mathbb{I}(Y=k) \cdot (w_k^\mathrm{T} X + b_k) \right)$$

其中 $\mathbb{I}(Y=k)$ 是示性函数（当 $Y=k$ 时为 1，否则为 0），$w_k$ 和 $b_k$ 分别是第 $k$ 类的权重和偏置。当我们只关心 $Y=k$ 这个特定类别时，上式可以简化为 $\varphi(k,X) = \exp(w_k^\mathrm{T}X + b_k)$。

将这个势函数代入条件概率公式中：

$$P(Y=k|X) = \frac{\varphi(k,X)}{\sum_{j=1}^K \varphi(j,X)} = \frac{\exp(w_k^\mathrm{T}X+b_k)}{\sum_{j=1}^K \exp(w_j^\mathrm{T}X+b_j)}$$

这就是 softmax 回归的公式

因此，从概率图模型的角度来看，logistic/softmax 回归相当于一个 势函数为特征的线性组合的指数形式的 Markov 随机场。这种直接对条件概率 $P(Y|X)$ 进行建模的模型，也称作判别式模型。