1 马尔可夫决策过程#
解答:
(1) 状态空间即手中金钱数量 S={0,10,20,30,40};
(2) 动作空间 A={停止,玩A,玩B};
(3) 转移概率 P:如下表所示。其中 S=0、S=40 是终止状态,当且仅当进入终止状态时停止游玩;S=20 是初始状态;S=10 时,由于玩 B 需要本金 20 元,因此该状态只能选择玩 A。
| 当前状态 s | 动作 a | 可能的结果 | 下一状态 s′ | 转移概率 Pss′a |
|---|
| 0 | 停止 | / | / | 1.00 |
| 10 | 玩 A | 赢10元 | 20 | 0.05 |
| | 输10元 | 0 | 0.95 |
| 20 | 玩 A | 赢10元 | 30 | 0.05 |
| | 输10元 | 10 | 0.95 |
| 玩 B | 赢10元 | 30 | 0.01 |
| | 输20元 | 0 | 0.99 |
| 30 | 玩 A | 赢10元 | 40 | 0.05 |
| | 输10元 | 20 | 0.95 |
| 玩 B | 赢10元 | 40 | 0.01 |
| | 输20元 | 10 | 0.99 |
| 40 | 停止 | / | / | 1.00 |
(4) 奖励函数:定义 0 状态的奖励为 0,40 状态的奖励为 40,其他状态的奖励为该次游玩后手中金钱的变化量。这导致模型会以尽可能少输钱的方式达到 40 元
2 Gridworld 小游戏#
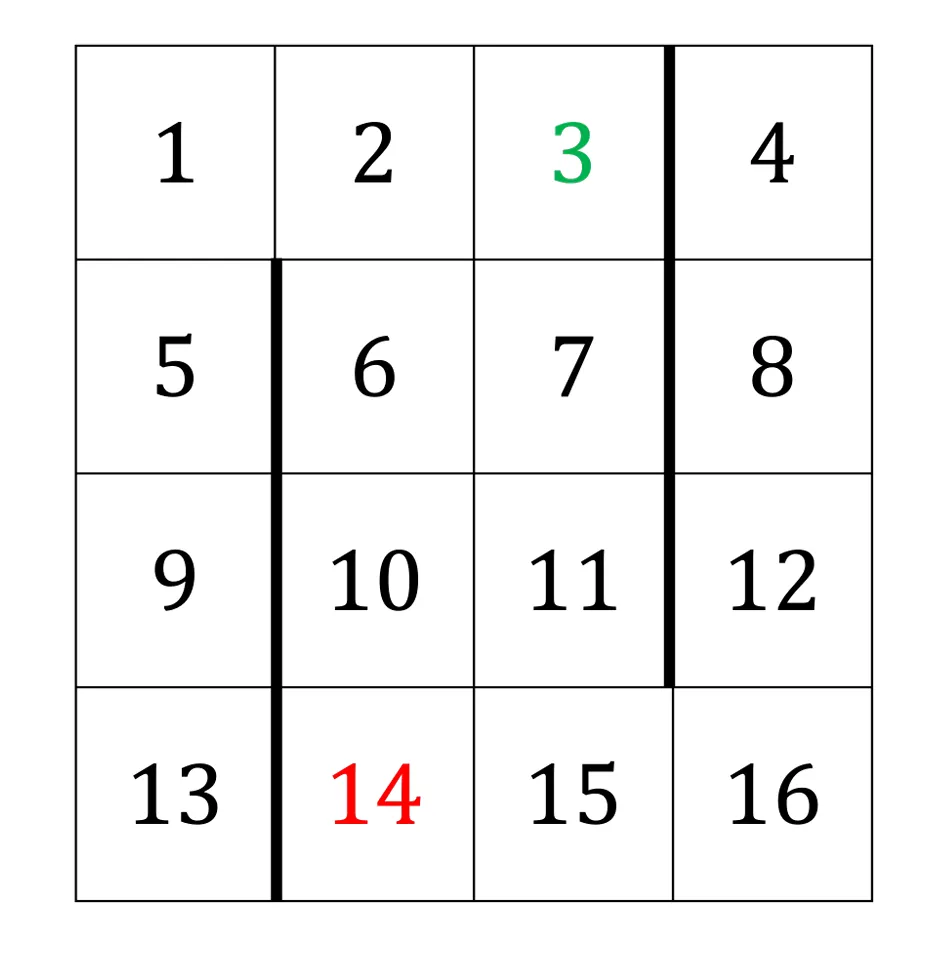
考虑如下的网格环境:
- 从任意非阴影的格子出发,你可以向上、向下、向左或向右移动。动作是是确定性的,意味着动作执行后一定会从一个状态到达另一个状态(例如从状态 13 向上走,可以连接到状态 9)。
- 较粗的边表示墙壁,尝试向墙壁方向移动将会导致智能体原地不动(例如从状态 13 向右走,无法到达状态 14,仍会停留在原状态 13)。
- 在绿色目标格子(编号 3)采取任何动作将获得奖励 rg(因此 r(3,a)=rg 对所有动作 a 成立),并结束回合。在红色死亡格(编号 14)采取任何动作将获得奖励 rr (因此 r(14,a)=rr 对所有动作 a 成立),并结束回合。
- 在其他所有格子中,采取任何动作都与奖励 rs∈{−1,0,+1} 相关(即使该动作导致智能体保持在原地)。
除了特殊规定外,以下假设折扣因子 γ=1,rg=+3,且 rr=−3。
2(a) 最短路径策略#
解答:
定义 rs=−1,即每走一格都给出一个负奖励,即对于最终奖励,将要扣除路程的长度。这样到达绿色目标的路径越短,路程上的损失越少,因此在最大化过程中,最优策略将会返回最短路径。
根据最短路观察,可定义策略 π:除了绿色和红色,在满足“使得到绿色目标格子距离减少”的所有允许动作中均匀随机选择;绿色和红色状态在所有允许动作中随机均匀选择。也即,记向上、下、左、右动作为 u、d、l、r,那么
π(u∣s)π(d∣s)π(l∣s)π(r∣s)=⎩⎨⎧10.50for s=5,7,9,11,13,15for s=6,10,14for s=1,2,3,4,8,12,16=⎩⎨⎧10.50for s=4,8,12for s=3for s=1,2,5,6,7,9,10,11,13,14,15,16=⎩⎨⎧10.50for s=16for s=3for s=1,2,4,5,6,7,8,9,10,11,12,13,14,15=⎩⎨⎧10.50for s=1,2for s=6,10,14for s=3,4,5,6,7,8,9,11,12,13,15,16
由状态价值函数的 Bellman equation,代入 rs=−1、γ=1 得,对一切 s=3 and 14
Vπ(s)=E[Rt+1+γVπ(St+1)∣St=s]=−1+E[Vπ(St+1)∣St=s]=−1+a∑π(a∣s)Vπ(s′)
注意到,对任意非红色格子,按照该策略进行一步移动,均导致离绿色目标格子的距离减小一格,因此对于 π=0.5 的情形,两个概率将合并;又进入绿色状态时 Vπ(3)=rg=+3,到达绿色状态的路径上每走一格奖励减 1,故记路程最短长度为 d(s),递推可得
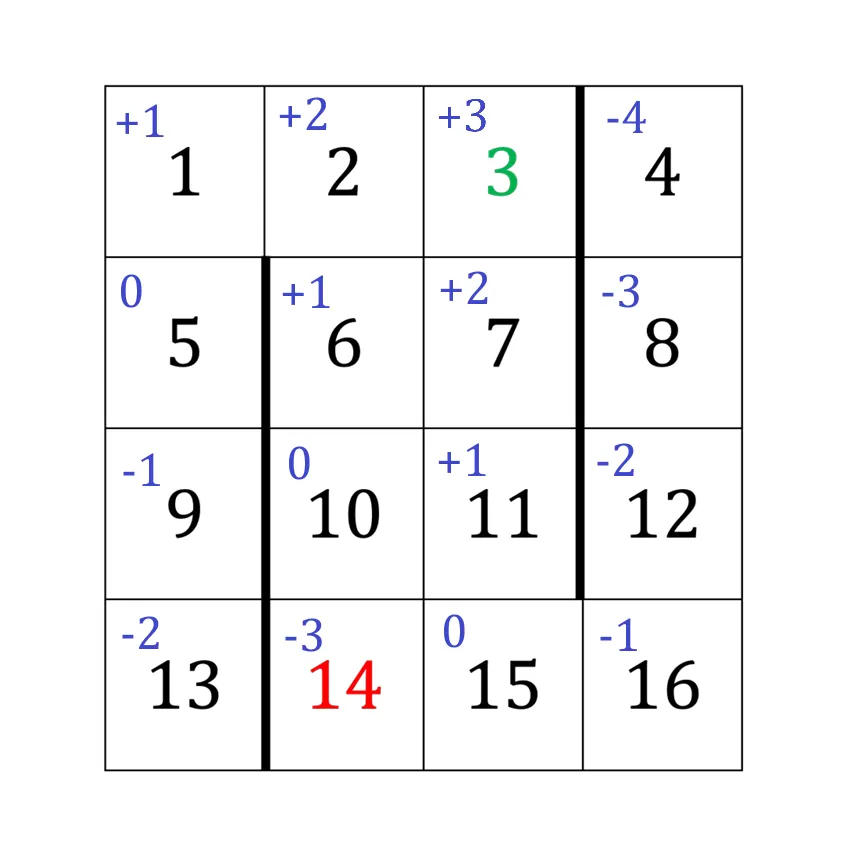
Vπ(s)=3−d(s),∀s=3 and 14
因此每个格子的最优价值,如图所示(左上角蓝色数字为最优价值)
2(b) 奖励变化的影响#
解答:
由题意,rs=1,递推后的状态价值函数为
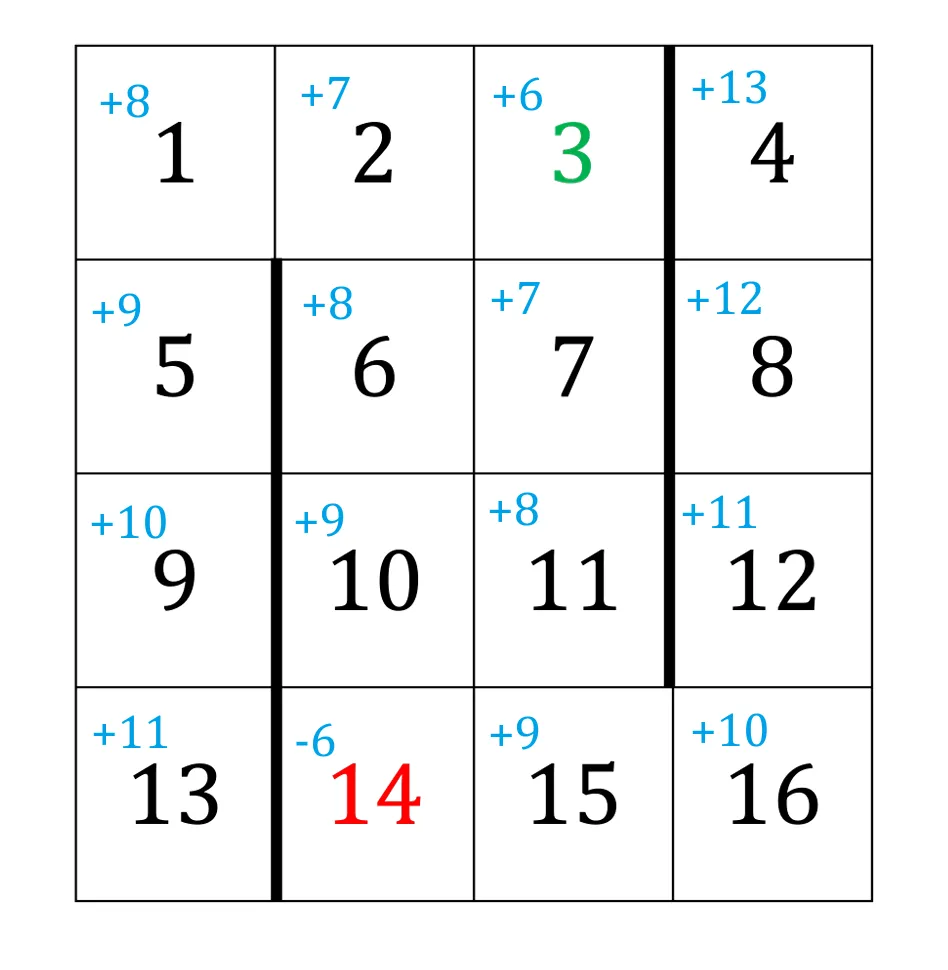
Vnewπg(s)=6+d(s),∀s=3 and 14
因此该网格世界中,每个格子的最优价值如图所示
2(c) 奖励变化的一般表达式#
解答:
对任意状态 s:
Vnewπ(s)=Eπ[Rnew,t+1+γVnewπ(St+1)∣St=s]=c⋅rs+γEπ[Vnewπ(St+1)∣St=s]
Voldπ(s)c⋅Voldπ(s)=Eπ[Rold,t+1+γVoldπ(St+1)∣St=s]=rs+γEπ[Voldπ(St+1)∣St=s]=c⋅rs+γEπ[c⋅Voldπ(St+1)∣St=s]
于是 Vnewπ(s)=c⋅Voldπ(s),由 Bellman equation 以及 2(a) 中关于概率合并的证明可得
Qπ(s,a)=Rsa+γs′∑Pss′aV(s′)=rs+γV(s′)
于是
Qoldπ(s,a)Qnewπ(s,a)=rs+γVoldπ(s′)=c⋅rs+γcVoldπ(s′)=c⋅Qoldπ(s,a)
对 Q 做最大化以得到最优策略。因此:
- 当 c≥0 时,最大化结果不变,策略不变
- 当 c<0 时,由于该网格世界不具有对称性,最优策略发生改变。
2(d) 正奖励的影响#
解答:
c=2−(−1)=3,于是 rg=+6,rr=0,γ=1 。这导致所有格子均有非负奖励,因此价值函数始终递增且发散到 +∞ 。故最优策略即“在循环路径中无限运动”,只要不进入红绿两个终止态,奖励的累积将会趋于正无穷。
此时非阴影格子的价值变为 +∞




